树状数组及线段树总结
区间更新,单点查询
树状数组:将原数组转化为差分数组,用树状数组维护差分数组,每次区间更新时只需要修改差分数组的首尾,单点查询时,求差分数组的前缀和就是原数组的单点值。更新和查询复杂度均为O(logn)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
using namespace std;
int A[N];
int tree[N];
int lowbit(int x) { return x & (-x); }
int n, m;
void add(int loc, int val) {
for (; loc <= n; loc += lowbit(loc)) {
tree[loc] += val;
}
}
int query(int loc) {
int sum = 0;
for (; loc; loc -= lowbit(loc)) {
sum += tree[loc];
}
return sum;
}
int main() {
cin >> n >> m;
int l, r, t;
char c;
memset(tree, 0, sizeof tree);
for (int i = 1; i <= n; i++) {
cin >> t;
add(i, t);
add(i + 1, -t);
}
for (int i = 1; i <= m; i++) {
cin >> c;
if (c == 'Q') {
cin >> t;
cout << query(t) << endl;
} else {
cin >> l >> r >> t;
add(l, t);
add(r + 1, -t);
}
}
}线段树:区间修改操作需要使用惰性标记,否则复杂度为O(n)。查询时逐层累加。
区间修改,区间查询
树状数组:只能用于求区间和。需要一些数学推导:
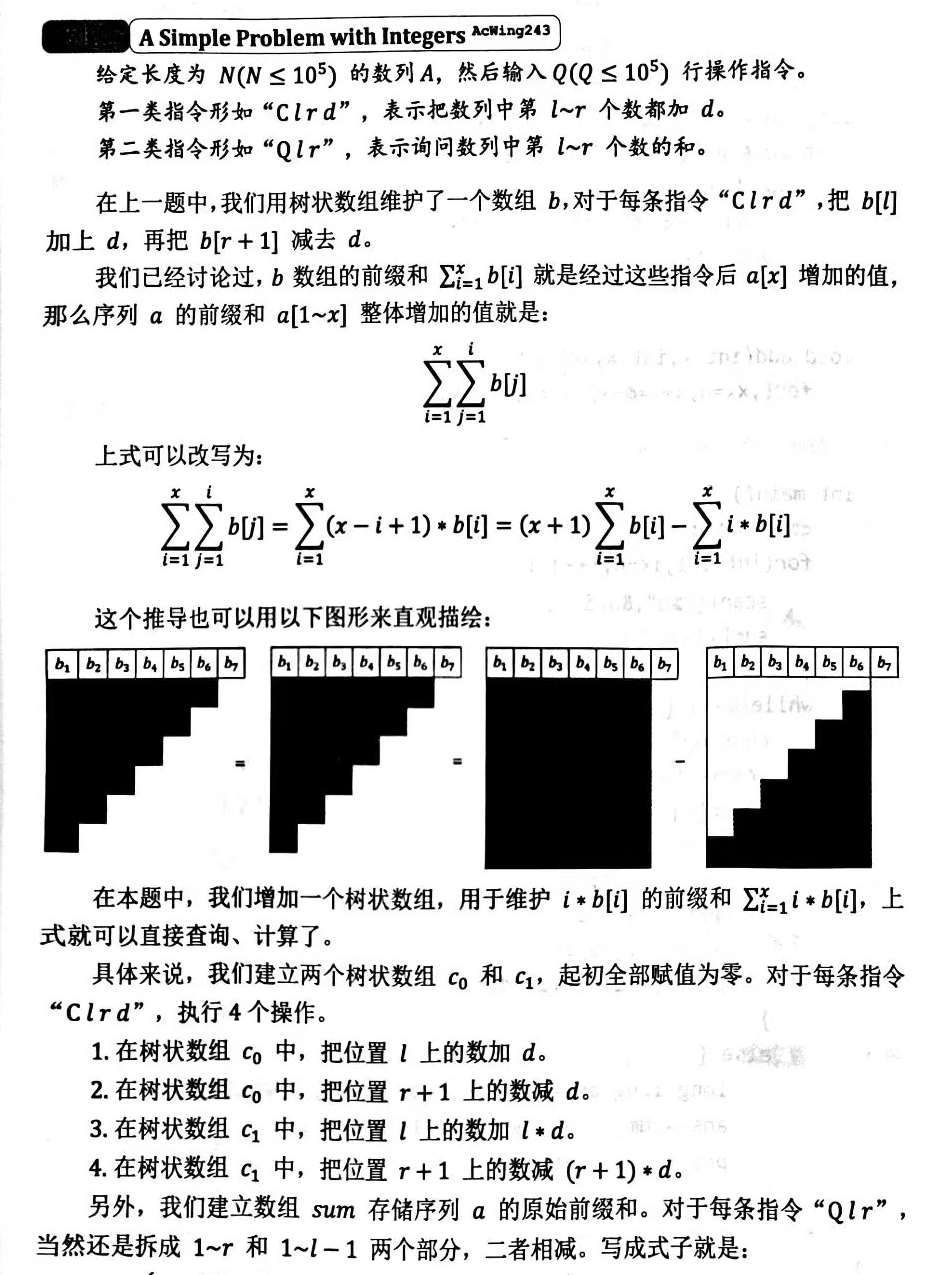
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
using namespace std;
int n, m;
int tree1[N], tree2[N];
int lowbit(int x) { return x & (-x); }
void add(int loc, int val, int tree[]) {
for (; loc <= n; loc += lowbit(loc)) {
tree[loc] += val;
}
}
ll query(int loc, int tree[]) {
ll sum = 0;
for (; loc; loc -= lowbit(loc)) {
sum += tree[loc];
}
return sum;
}
ll presum(int x) { return (x + 1) * query(x, tree1) - query(x, tree2); }
int main() {
int l, r, t;
cin >> n >> m;
memset(tree1, 0, sizeof tree1);
memset(tree2, 0, sizeof tree2);
for (int i = 1; i <= n; i++) {
cin >> t;
add(i, t, tree1);
add(i + 1, -t, tree1);
add(i, i * t, tree2);
add(i + 1, -(i + 1) * t, tree2);
}
char c;
for (int i = 1; i <= m; i++) {
cin >> c;
if (c == 'Q') {
cin >> l >> r;
cout << presum(r) - presum(l - 1) << endl;
} else {
cin >> l >> r >> t;
add(l, t, tree1);
add(r + 1, -t, tree1);
add(l, l * t, tree2);
add(r + 1, -(r + 1) * t, tree2);
}
}
}线段树:
使用惰性标记。
可以通过转化为差分数组,对原数组进行区间修改转化成对差分数组进行单点修改。
-
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
using namespace std;
ll bit[N];
ll bs[N];
int n, m;
struct Tree {
int l, r;
ll data;
} ts[N * 4];
ll gcd(ll x, ll y) {
if (y < 0) y = -y;
if (x < 0) x = -x;
if (x < y) swap(x, y);
if (y == 0) {
return x;
}
return gcd(y, x % y);
}
void build(int p, int l, int r) {
ts[p].l = l, ts[p].r = r;
if (l == r) {
ts[p].data = bs[l];
return;
}
int mid = (l + r) >> 1;
build(p * 2, l, mid);
build(p * 2 + 1, mid + 1, r);
ts[p].data = gcd(ts[p * 2].data, ts[p * 2 + 1].data);
}
int lowbit(int x) { return x & (-x); }
void add_bit(int loc, ll val) {
for (; loc <= n; loc += lowbit(loc)) {
bit[loc] += val;
}
}
ll query_bit(int loc) {
ll sum = 0;
for (; loc; loc -= lowbit(loc)) {
sum += bit[loc];
}
return sum;
}
void update(int p, int loc, int val) {
if (ts[p].l == ts[p].r) {
ts[p].data += val;
return;
}
int mid = (ts[p].l + ts[p].r) >> 1;
if (loc <= mid) {
update(p * 2, loc, val);
} else {
update(p * 2 + 1, loc, val);
}
ts[p].data = gcd(ts[p * 2].data, ts[p * 2 + 1].data);
}
ll query(int p, int l, int r) {
if (l <= ts[p].l && r >= ts[p].r) {
return abs(ts[p].data);
}
int mid = (ts[p].l + ts[p].r) >> 1;
ll ret = 0;
if (l <= mid) {
ret = gcd(query(p * 2, l, r), ret);
}
if (r > mid) {
ret = gcd(query(p * 2 + 1, l, r), ret);
}
return ret;
}
int main() {
cin >> n >> m;
memset(bit, 0, sizeof bit);
ll pre = 0, t;
for (int i = 1; i <= n; i++) {
cin >> t;
bs[i] = t - pre;
pre = t;
add_bit(i, bs[i]);
}
char c;
ll l, r, d;
build(1, 1, n);
for (int i = 1; i <= m; i++) {
cin >> c;
if (c == 'C') {
cin >> l >> r >> d;
add_bit(l, d);
add_bit(r + 1, -d);
update(1, l, d);
if (r + 1 <= n) update(1, r + 1, -d);
} else {
cin >> l >> r;
cout << gcd(query_bit(l), query(1, l + 1, r)) << endl;
}
}
}
单点修改,区间查询
树状数组:树状数组最原始的应用。
线段树:
-
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
using namespace std;
int n, m;
struct Tree {
int l, r;
int maxsum, lsum, rsum, sum;
} ts[N * 4];
int As[N];
void build(int p, int l, int r) {
ts[p].l = l;
ts[p].r = r;
if (ts[p].l == ts[p].r) {
ts[p].sum = ts[p].maxsum = ts[p].lsum = ts[p].rsum = As[l];
return;
}
int mid = (l + r) >> 1;
build(p * 2, l, mid);
build(p * 2 + 1, mid + 1, r);
ts[p].sum = ts[p * 2].sum + ts[p * 2 + 1].sum;
ts[p].lsum = max(ts[p * 2].lsum, ts[p * 2].sum + ts[p * 2 + 1].lsum);
ts[p].rsum = max(ts[p * 2 + 1].rsum, ts[p * 2 + 1].sum + ts[p * 2].rsum);
ts[p].maxsum =
max(ts[p * 2].maxsum,
max(ts[p * 2 + 1].maxsum, ts[p * 2].rsum + ts[p * 2 + 1].lsum));
}
ll lquery(int p, int l, int r) {
if (l <= ts[p].l && r >= ts[p].r) {
return ts[p].lsum;
}
int mid = (ts[p].l + ts[p].r) >> 1;
ll ret = lquery(p * 2, l, r);
if (r > mid) {
ret = max(ret, ts[p * 2].sum + lquery(p * 2 + 1, l, r));
}
return ret;
}
ll rquery(int p, int l, int r) {
if (l <= ts[p].l && r >= ts[p].r) {
return ts[p].rsum;
}
int mid = (ts[p].l + ts[p].r) >> 1;
ll ret = rquery(p * 2 + 1, l, r);
if (l <= mid) {
ret = max(ret, ts[p * 2 + 1].sum + rquery(p * 2, l, r));
}
return ret;
}
ll query(int p, int l, int r) {
if (l <= ts[p].l && r >= ts[p].r) {
return ts[p].maxsum;
}
int mid = (ts[p].l + ts[p].r) >> 1;
ll ret = INF;
if (l <= mid) {
ret = max(ret, query(p * 2, l, r));
}
if (r > mid) {
ret = max(ret, query(p * 2 + 1, l, r));
}
if (l <= mid && r > mid) {
ret = max(rquery(p * 2, l, r) + lquery(p * 2 + 1, l, r), ret);
}
return ret;
}
void change(int p, int x, int y) {
if (ts[p].l == ts[p].r) {
ts[p].sum = ts[p].maxsum = ts[p].lsum = ts[p].rsum = y;
return;
}
int mid = (ts[p].l + ts[p].r) >> 1;
if (x <= mid) {
change(p * 2, x, y);
} else {
change(p * 2 + 1, x, y);
}
ts[p].sum = ts[p * 2].sum + ts[p * 2 + 1].sum;
ts[p].lsum = max(ts[p * 2].lsum, ts[p * 2].sum + ts[p * 2 + 1].lsum);
ts[p].rsum = max(ts[p * 2 + 1].rsum, ts[p * 2 + 1].sum + ts[p * 2].rsum);
ts[p].maxsum =
max(ts[p * 2].maxsum,
max(ts[p * 2 + 1].maxsum, ts[p * 2].rsum + ts[p * 2 + 1].lsum));
}
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i++) {
cin >> As[i];
}
build(1, 1, n);
int k, x, y;
for (int i = 1; i <= m; i++) {
cin >> k >> x >> y;
if (k == 1) {
if (x > y) swap(x, y);
cout << query(1, x, y) << endl;
} else {
change(1, x, y);
}
}
}
-
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 Sprooc!
评论
